From MLOps to point-of-sale: Merkle proofs and data locality
Necessity is the mother of invention, and to move from complex orchestrated cloud services to unstoppable protocols, we must transition from a location-centric model to one that emphasizes location-independent verifiable links. Immutable data structures and cryptographic proofs emerge as key components in this new paradigm, providing the means to verify that data remains unaltered during storage or transmission, a critical feature for managing and maintaining data integrity across diverse applications. In this new world accessibility, data integrity, and performance are all underpinned by the same mathematical foundations.
Take, for instance, an AI model that's engaged in a healthcare application—perhaps a diagnostic tool. The training process for such a model would involve large amounts of sensitive patient data, which must remain unaltered and confidential to ensure accurate diagnoses and maintain patient privacy. A slight alteration in the training data could lead to drastically different—and potentially erroneous—diagnostic outputs.
This is where the cryptographic proofs step in. By creating a tamper-proof data structure that stores the intermediate results of the data pipeline and their relationships, the integrity of the training data used in these models can be robustly verified. Any change in the data pipeline, such as an update or alteration to the training data, would necessitate the recomputation of only the affected parts of the tree. The rest of the results remain intact and reusable, and their integrity verifiable against their respective proofs. This generalizes especially well to use cases like tracking LoRA fine-tuning layer provenance.
Merkle Trees, which are also known as hash trees, are foundational to technologies like system software, blockchains and file sharing. Their primary purpose is to verify the integrity of data, and they do this in a way that significantly diminishes the amount of work required to confirm large data structures.
This approach is not only time-efficient and resource-saving but the automatic provenance tracking also enhances debugging and auditing capabilities when working with AI training sets and model outputs. As a result, if the AI diagnostic tool provides an unexpected output, it would be possible to trace back through the data pipeline, verifying the integrity of the data at each step. This traceability is possible because of the proofs and the Merkle tree data structure.
Moreover, including details such as prompts, random seeds, and model specifics in the proof Merkle hash allows for a comprehensive representation of a particular computational session. This comprehensive representation provides evidence that certain outputs originated from a specific session and were not tampered with, further boosting the security, efficiency, and transparency of AI and distributed systems.
Git and BitTorrent’s use of Merkle Trees
The reliability of proofs in data systems is vital for replication and sync strategies, seen in peer-to-peer (P2P) file-sharing networks. In these networks, verifiable references and proofs ensure data consistency across nodes. This is evident in BitTorrent, where Merkle Trees facilitate efficient data verification, reduce torrent file size, and allow flexible verification, enhancing data transfer and reliability.
Immutable data structures like content-addressed public data graphs and trees, offer benefits such as traceability, data integrity, and efficient caching. These structures create unique versions of data with each change, ideal for systems prioritizing data integrity.
Distributed version control systems (DVCS), like Git, exemplify the use of immutable data structures. In DVCS, each change or 'commit' generates a new immutable snapshot of the codebase, forming a chain of verifiable references. This provides traceability and control over the codebase, enabling users to authenticate each change and revert to a previous state if needed.
Git uses Merkle trees to manage changes in files, directories, and commits. These trees consist of unique labels or hashes for each node, with root labels derived from a cryptographic hash. Git manages file content through 'blob objects', identified by a Secure Hash Algorithm (SHA-1) hash. 'Tree objects' represent directories, including entries for each file or subdirectory. 'Commit objects' encapsulate author information, the commit message, and pointers to the tree object and parent commits.
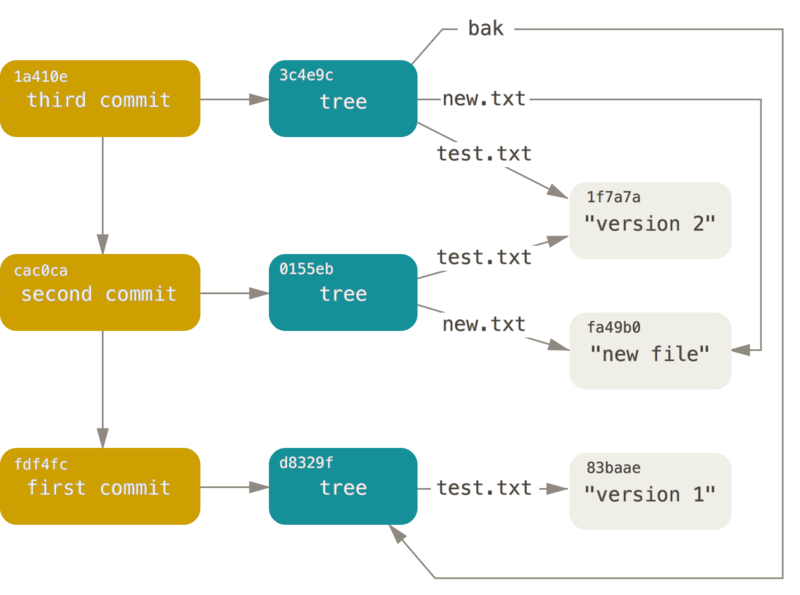
Git's use of Merkle trees allows efficient change tracking, corruption identification, and comparison of repository versions. If a single file changes in a codebase, Git only needs to create a new blob for that file, update the relevant tree objects, and create a new commit pointing to the new root tree. Unchanged files continue to be represented by existing objects in the Git database. This space-efficient method also speeds up operations like commit comparisons and branch merging.
In summary, Git utilizes Merkle trees to efficiently and securely manage version control. The immutable nature of the objects and the cryptographic verification ensure a robust version control system, making Git an industry standard in managing codebases.
Immutable B-trees and Merkle Trees
B-trees are a staple of data management, but mutations present challenges, particularly in systems that require high concurrency or involve complex data structures. In such scenarios, updating mutable B-trees can lead to conflicts or require complex locking mechanisms to maintain data integrity, thereby decreasing performance and scalability. To developers, this shows up as global locks or corrupt data.
In contrast, immutable B-trees offer an elegant solution to these challenges. By treating every change as a new version of the data structure, conflicts are eliminated, and concurrent updates become straightforward. This model of immutability is particularly advantageous in content management systems (CMS), where versioning and rollback capabilities are crucial. In an immutable B-tree-based CMS, every update or addition creates a new, distinct version of the content tree, allowing users to easily track changes, compare different versions, and revert changes when necessary. The rise of git-based CMSs shows this is a powerful combination.
Immutable Merkle trees extend the idea of content-addressed structures by linking each node to its children through their cryptographic hashes. This feature creates a tree where the root node's hash effectively serves as a summary of the entire tree's content. If any part of the tree changes, the root hash also changes, making Merkle trees inherently resistant to tampering and ideal for verifying large or complex data structures efficiently.
Merkle trees are foundational in Blockchain technologies, forming the heart of the decentralized and secure nature of these systems. Each block in a blockchain is linked to its predecessor through a hash, forming a chain of blocks (hence the name), which is essentially a Merkle tree. The root of the tree, known as the block's hash, encapsulates the integrity of the entire block and its transaction history.
To illustrate, consider the structure of a Merkle tree:
ROOT=H(H(A+B)+H(C+D))
/ \
H(A+B) H(C+D)
/ \ / \
A B C D
In this tree, A, B, C, and D are data blocks. H(A+B) and H(C+D) are the parent nodes, created by hashing the concatenated hashes of their child nodes. The root node is the hash of the concatenated hashes of its children, providing a summary of the entire tree.
Let's illustrate this with a simple code snippet showing a basic implementation of a content-addressed tree:
class TreeNode:
def __init__(self, value, left=None, right=None):
self.value = value
self.left = left
self.right = right
self.hash = self.compute_hash()
def compute_hash(self):
left_hash = self.left.hash if self.left else ''
right_hash = self.right.hash if self.right else ''
return hashlib.sha256(f'{self.value}{left_hash}{right_hash}'.encode()).hexdigest()
In this Python code, each TreeNode represents a node in a binary tree, with a value and links to its left and right children. The hash of each node is computed from its value and the hashes of its children, effectively creating a content-addressed tree where any change to a node or its descendants results in a new, unique hash.
Merkle trees offer significant benefits for data replication, synchronization, and management. For instance, in the context of verifiable user-owned profiles on a content delivery network, Merkle trees can ensure data integrity and verify data ownership. Each user's profile can be structured as a Merkle tree, where the root hash serves as a unique, verifiable identifier for the profile. This approach allows the network to verify and synchronize user profiles across different nodes efficiently, ensuring data consistency and verifiability at all times. Merkle trees also allow for efficient replication, as any two root hashes can be used to compute a diff, and only the necessary blocks need to be moved.
Use case: Mobile point of sale with cloudless analytics
In today's digital landscape, robust and reliable data management systems are essential. Mobile point of sale (POS) systems, operating at the network edge, are well-suited for advanced data structures like immutable Merkle trees, and stand to benefit from features like secure components and cloudless analytics.
Utilizing Fireproof’s location independence, the application conducts analytics locally, enhancing performance and resilience by reducing cloud reliance. This design significantly cuts latency and increases the responsiveness of real-time applications. Data integrity is assured through Fireproof's hash-verifiable data and immutable structures, ensuring system reliability even during network disruptions. The results of on-device analytics queries can be replicated to the application’s cloud, and any interesting results can be traced back to the source without worry about data integrity.
Fireproof's location independence facilitates effective resource distribution. New functions can be distributed to all POS systems, enabling result collection without replicating entire datasets. This optimizes computational resources and reduces data transfer overhead—a key advantage in bandwidth-limited environments.
The system's integration of Merkle CRDTs (conflict-free replicated data types) enhances these benefits. Applications can sync lightweight query results with deterministic references to source data, eliminating the need to replicate source data. This ensures data consistency and provability across multiple nodes or systems, irrespective of data storage or processing location. It also means your backups can be stored regionally while your synced queries are archived elsewhere for performance and auditablity. Operational movement is dramatically simplified by the fact that the same source data set has the same hash address, deterministically.
Merkle Diffs and CRDTs
Merkle Diffs and CRDTs are essential to cloudless computing and location-independent data structures. These two elements are used today in real-time collaboration tools and significantly enhance their performance and reliability.
Merkle Diffs optimize data synchronization between nodes in a distributed system. They work by comparing the Merkle trees of two nodes and identifying the differences or "diffs". These diffs are then used to update the nodes, ensuring data consistency across the network. This method is significantly more efficient than transferring entire datasets, especially for large data structures. Fireproof uses this concept to enable real-time collaboration and multi-user sync.
CRDTs also play a crucial role in conflict resolution and fork management in distributed systems. Essentially, a CRDT is a data structure that allows multiple replicas to be updated independently and concurrently without coordination between them. Later, these replicas can be merged with guaranteed eventual consistency. This deterministic conflict resolution is critical in real-time collaboration tools like Fireproof, where simultaneous edits by multiple users are common. All Merkle diffs are CRDTs, allowing the eventual consistency advantages to compound at scale.
In these collaborative platforms, users can make changes to the shared document or data structure independently. When they reconnect to the network, the changes are merged using CRDTs, ensuring that no updates are lost and all users eventually see the same final state. It's a seamless process that provides an uninterrupted user experience, even in the face of network inconsistencies or disconnections.
CRDTs enhance robustness, scalability, and fault tolerance. They enable distributed systems to function efficiently without the need for a central authority or constant communication between nodes, making them ideal for scenarios where network latency or intermittent connectivity may be an issue.
Immutable Prolly Trees
Building upon the principles of Merkle trees, let's now traverse into the realm of immutable prolly trees, a potent data structure whose capabilities are slated to transform future applications. The mobile point-of-sale example offered above relies on the replication and sync properties of prolly trees.
An immutable prolly tree, as its name suggests, is a tree data structure that is append-only - once data is written into it, it can't be modified. It also addresses its inner blocks by hash address, like a Merkle tree. This approach provides certain advantages, such as simplified versioning, reduced contention in concurrent systems, and improved crash recovery. This makes the prolly tree a perfect fit for systems that demand stringent data integrity. The challenge it overcomes is how to do all of that, but also have root hashes that are stable regardless of insertion order. The same data set gets the same address, no matter what. This is necessary for peer-to-peer replication, without it, a small data set can take forever to replicate, as there is no way for peers to determine if they have the same content. Without hash stability, you can also end up with major write amplification, as small changes can cascade through the whole tree. Read on to learn how prolly trees solve this.
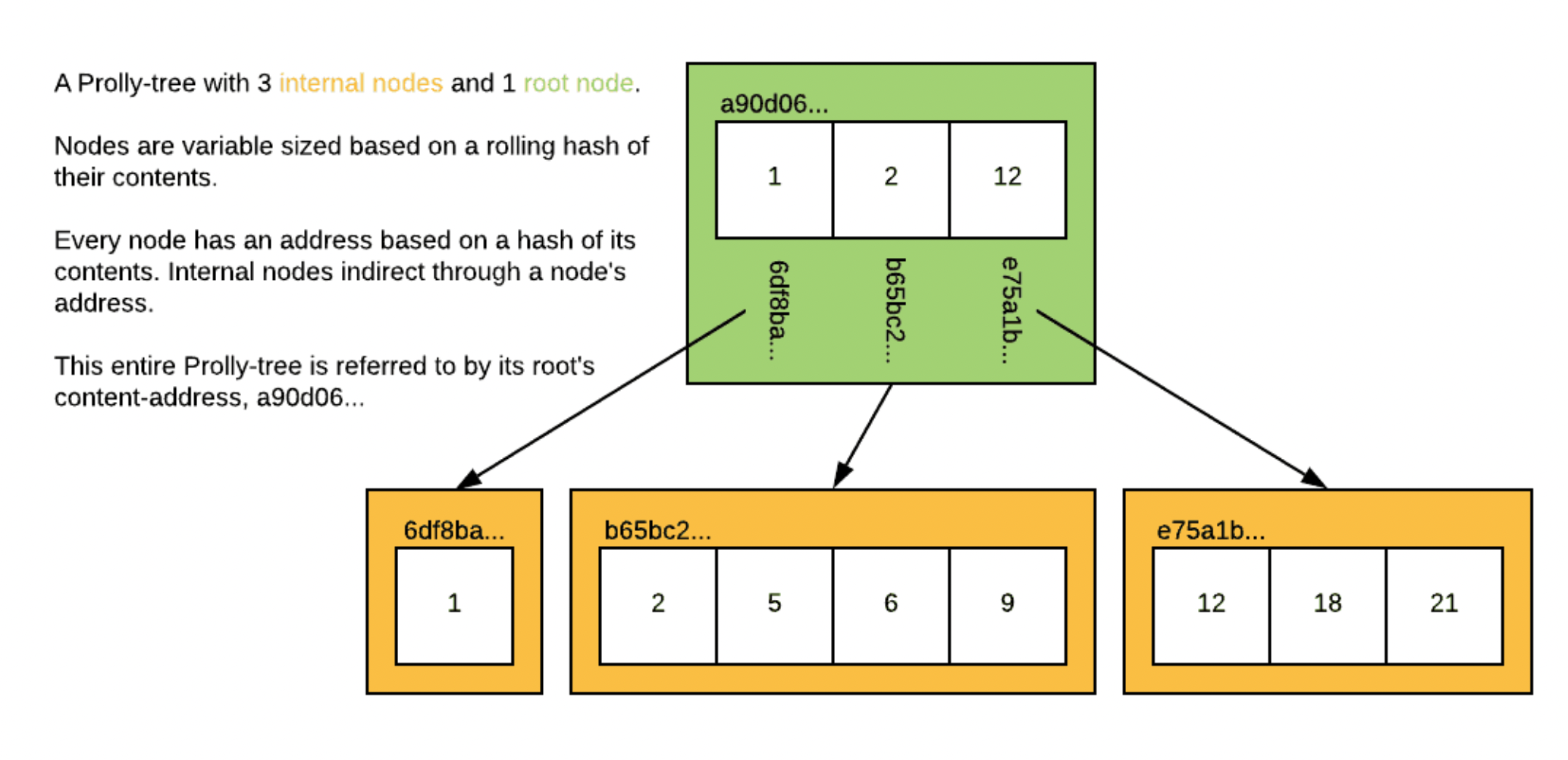
Figure from DoltDB's deep dive.
Here's a step-by-step guide on how updates work in an append-only immutable Prolly Tree:
- Search: Locate the leaf node where the key-value pair would be inserted if it were a traditional tree. Traverse the tree from the root node, following the appropriate child pointers based on the key comparisons, until you reach the desired leaf node.
- Copy: Create a new leaf node that is a copy of the existing leaf node, but with the new key-value pair inserted in the appropriate position, maintaining the sorted order of the keys within the node.
- Chunking: Apply the chunking function to the modified leaf node to ensure that the tree structure remains consistent and history-independent. If the chunking function causes the leaf node to split, create new leaf nodes accordingly.
- Update parent: Copy the parent node of the modified leaf node and update the child pointer to point to the new leaf node created in step 2 or the new leaf nodes created in step 3. If the parent node was already pointing to the original leaf node, the update is complete. Otherwise, continue to step 5.
- Propagate changes: Continue updating parent nodes up the tree, applying the chunking function as needed, until you reach the root. If the root node needs to be split, create a new root node with the appropriate child pointers.
- Update tree reference: Point the prolly tree reference to the new root node, completing the update.
By following these steps, the append-only immutable Prolly Tree modifies records without changing existing data. This creates a persistent data structure that maintains previous versions of the tree and simplifies various operations in concurrent and distributed systems. Additionally, the chunking function employed by Prolly Trees ensures history independence, minimizes write amplification, and optimizes data storage for improved performance.
The immutable nature of Prolly Trees bestows them with several distinctive benefits. First, they offer impeccable versioning capabilities. Each version of the data remains intact and accessible, serving as a detailed and reliable history of data changes over time.
Second, the Prolly Tree excels in concurrency management. Multiple operations can be performed concurrently without the risk of data conflicts or inconsistencies, making it an excellent choice for collaborative environments. Each operation is a function from the previous root to the new root, and merges are cheap so that you can bring together multiple trees into a single query at runtime.
Lastly, in the event of a crash, recovery is straightforward. Since each operation results in a new tree version, you can quickly revert to the previous stable state without data loss.
Although Merkle Search Trees and Prolly Trees are promising, it's worth noting that there are still challenges to be addressed. For instance, they aren't currently secure against adversarial inputs. A malicious actor could potentially exploit the hash function to overflow a block or artificially inflate the tree height.
Chunking in Prolly Trees
The chunking function in a Prolly Tree divides key-value pairs into discrete nodes or "chunks" within the tree, optimizing data storage, and enabling efficient comparisons between different tree revisions. The chunking function serves three main functions:
- Determinism and history independence: This means that a set of elements will always form the same tree, regardless of the order they were inserted. This invariant requires that the tree's structure must be a deterministic function of the contents of the tree.
- Minimizing write-amplification and maximizing structural sharing: The chunking function minimizes the amount of data that needs to be written or rewritten when a tree is updated. By maintaining stable chunk boundaries between revisions, the function ensures that only the portions of the tree that are affected by a change need to be updated, reducing the amount of data that needs to be written to disk or processed during merges.
- Balancing chunk size distribution: The chunking function aims to create a balanced distribution of chunk sizes, minimizing variance and enabling predictable performance for reading and writing data. Ideally, the function should create chunks that are neither too large nor too small, reducing the likelihood of performance issues arising from IO operations on disk.
The chunking function in a Prolly Tree works as follows:
- Key-value pairs are sorted into a sequence, which forms level 0 of the tree.
- This sequence is divided into discrete leaf nodes using a chunking algorithm that takes the key-value sequence as input and gives a boolean output of whether the current "chunk" should end after the current key-value pair.
- Next, a new sequence of key-value pairs is created from the last key of each leaf node and the content address of that node.
- This sequence is again chunked using a rolling hash and forms level 1 of the tree.
- The process continues until a level with a single root chunk is reached.
For prolly trees, chunk boundaries occur when the values of a rolling-hash function match a specific, low-probability pattern. This technique is referred to as content-defined chunking. Rolling-hash functions are suitable for this purpose because they are deterministic (i.e., history-independent) and make decisions locally.
The chunking function in a prolly tree must be resilient to the boundary-shift problem. In other words, it should not cause a cascade of boundary changes when an element is inserted or removed from the sequence. This stability is essential for minimizing write-amplification and maximizing structural sharing between tree revisions. Read more about prolly tree chunking and see the source of some of the figures in this article.
The Payoff: Location Independence and Data Synchronization
Location independence is the ability to access, process, and manipulate data irrespective of its physical location, improving accessibility and data processing efficiency. But without immutability and cryptographic proofs, location independence doesn’t offer much. Adding proofs to immutable data structures creates many opportunities to optimize end-user workflows.
Each Fireproof read or write operation is accompanied by a cryptographic proof – essentially a list of content identifiers (CIDs) that represent blocks read, added, or removed during the operation. This proof acts as a verifiable record of the transaction, ensuring data integrity and establishing trust between entities. Moreover, it allows for the execution of queries locally, provided that all the blocks referenced in the proof are available. This approach fosters efficient data retrieval and manipulation while maintaining data integrity and verifiability.
User-Centric Data Subsetting
User-centric data subsets can be easily created using the proofs associated with application-determined queries which generate a unique subset of data for each user, effectively creating a personalized database. The proof accompanying each query ensures that the resulting data subset is verifiable, promoting data integrity and trust. This process allows for targeted data operations, making it possible to deliver tailored services and recommendations based on individual users' data, but still absorb offline changes back to the main dataset.
Resource-optimized Subsets for Constrained Devices
Further refinement can occur by creating even smaller subsets from the initial user-specific database, targeting constrained devices. These devices often have limited processing power and storage capacity, necessitating efficient data structures. The creation of a device-specific data subset, optimized based on device constraints, ensures efficient data management and a smoother user experience on these devices. Again, the associated proofs guarantee the integrity of data operations, from the extraction of the smaller subset to its use on the device.
Event-Stream Integration of User Writes
Incorporating user writes into the larger dataset as an event stream makes processing offline updates asynchronously into a reliable operation. Here, the proof accompanying each write operation serves as a record of the transaction, ensuring data integrity during the process. This method is particularly beneficial for updating the main dataset without causing unnecessary latency or processing overhead. It also allows for effective tracking and synchronization of changes, offering git-like interfaces for power users.